失われた30年を、40年、50年としないために。
ー科学技術力に裏打ちされた経済大国の復興に向けてー

理科教育振興法は「値をダメにするな。ダメにした値は使えない。」という教えが主流であったとき、
科学技術基本法は「信用できなくした位を四捨五入する。」という教えに統一されるときの法律です。
また、大小多少の量感に加え、筆算を用いた実数量感育成が半世紀前にありましたが、
有理数量感へ
変わりました。研究教育者の測定値の扱い方の変化も、科学と産業の停滞に影響していると考えます。
科学や産業の停滞の原因が研究費や研究環境の違いだけであれば、敗戦直後の違いの方が大きいから、
世界一の技術を、多く、日本が持つことは出来なかったはずです。停滞要因が他にもあると考えます。
考えの基となるデータが誤っていると正しい答えは得られません。研究開発費の総額や伸び率の違い
だけでなく、測定値の扱い方の基礎の基礎部分が崩れていることも一因と考えます。
(産業の停滞は先進国から学んだ科学技術や日本先行の科学技術を磨き上げる速度が遅くなった為?)
失われた10年は量を測定する能力の低下、30年はその能力を育成する能力の低下が要因と考えます。
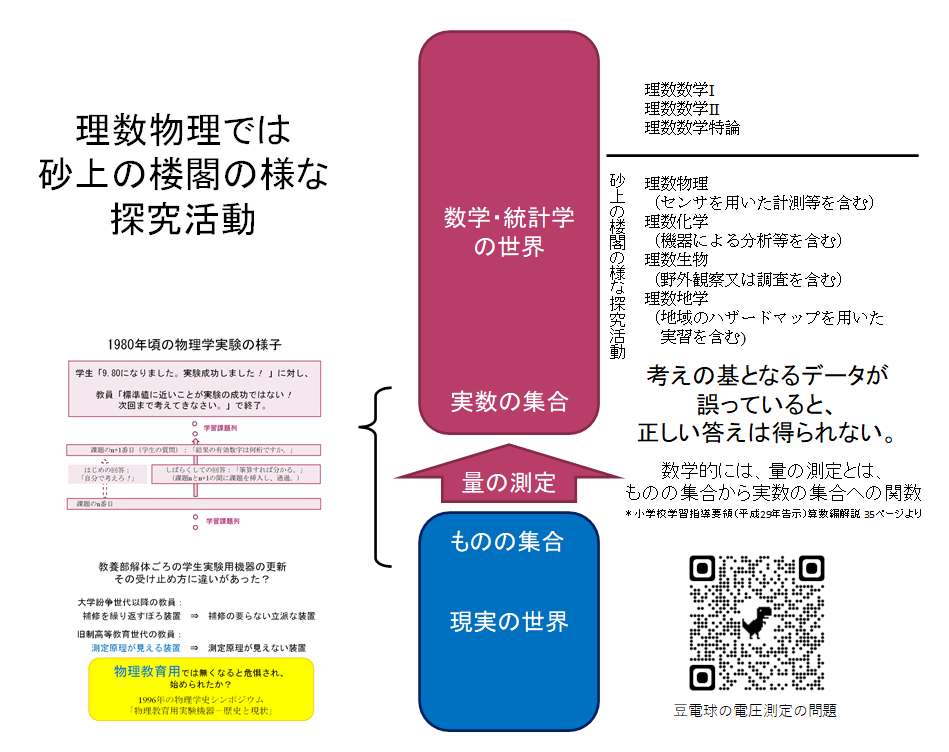
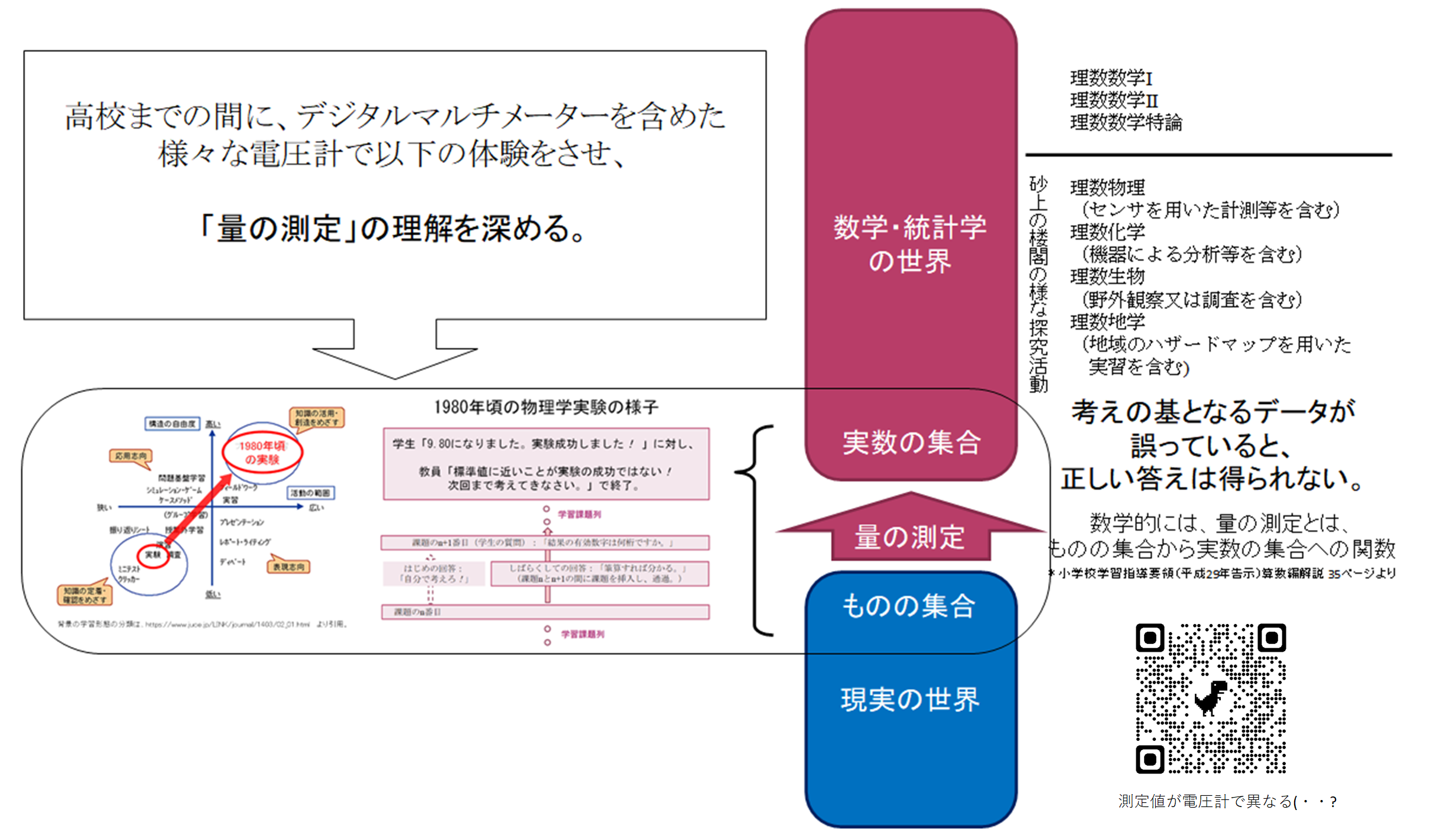
学習指導要領解説算数編の35頁に「量の測定とは、ものの集合から実数の集合への関数」とあります。
また、関数は関数でも、一価関数でないと現実の世界を数学の世界へ正しく写せないと考えます。
長さなどの量も円周率と同じ実数であり、大小や多少の量感に加え、実数としての量感育成も大切です。
適性のある学生に、現在、「量を測定する力を育成する力の低下」が負の影響を与えていると思います。
量の計算規則を覚えることではなく、実数としての量感育成のもとでの有効数字の気付きが大事です。
測定装置のブラックボックス化の中、高校に理数科目ができ、1980頃にあった物理教育の代わりを
小学校教育に再生しなければならなくなりましたが、逆センスの領域の見直しが行われたと考えます。
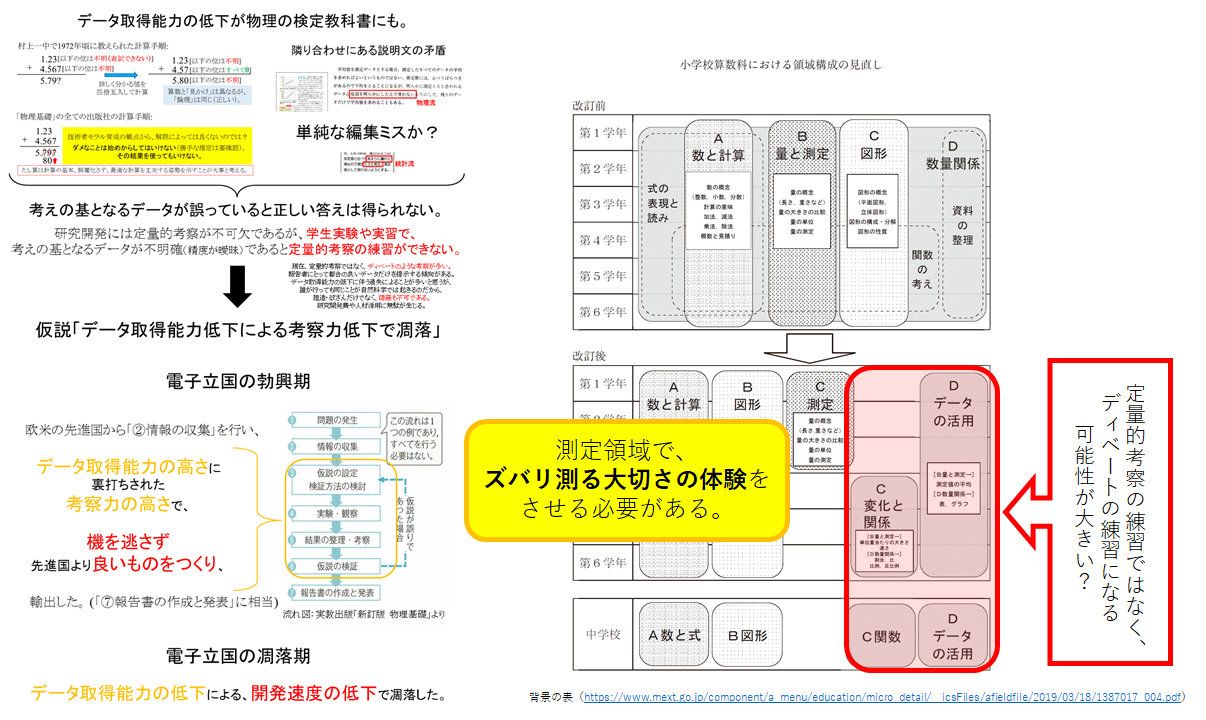
探究の進め方がどんなに良くとも、考えの基となるデータが誤っていると正しい答えは得られません。
探究の課題設定がどんなに良くとも、正しい答えが得られなければ、偽りの成果しか得られません。
データの活用では、先ず、定量的考察力の育成(平均値⇒確率誤差⇒カイ二乗検定、など)を行い、
次に、ディベート力の育成を計った方が良いと考えます。
硬貨の直径測定にも平均値の推定や検定が必要ですが、残差の2乗和も曖昧なままでのデータ活用に
なっており、砂上の楼閣の様な探究活動となり、ディベート力の育成になってしまっています。また、
理科教育振興法は「値をダメにするな。ダメにした値は使えない。」という教えが主流であったとき、
科学技術基本法は「信用できなくした位を四捨五入する。」という教えに統一されるときの法律です。
この教え方の違いが大きく影響し、前者と異なり、後者は経済成長には繋がらなかったと考えます。
理科に分類される分野の探究活動では、先ず、考えの基にできるデータの取得能力の育成が必要です。
小学校算数科における領域構成の見直しがものづくりに及ぼす影響に、今後、注意が必要と思います。
自然科学の場合、ジャッジが人ではないので、定量的に考えるためのデータの取得が大事になります。
学生実験の定量的実験力の育成につながっていた「量と測定」の柱が折れてしまったように見えます。
半世紀前は「値をダメにするな、ダメにした値は使えない。」と教えられました。今と異なります。
大学紛争で、学生実験や実習が大きな影響を受けました。講師以上で大学に採用された方は先輩教員
から指導を受けることはありませんでした(着任時から一国一城の主?の様)。その為、その影響が
大学教育に始めに出て、採用されてもしばらくは先輩教員から指導を受ける小学校などの先生方にも、
その影響が遅れて出た為、今、「量と測定」の柱が折れたとも考えられます。


測定原理の見える装置を使っての実験が多く、実験の成功とは何かを考えさせる課題も出されました。
物理学の自然法則は人の考えに無関係だから、数学や統計学を応用する前のデータの吟味が大切です。
定量的に考えるためのデータ取得が出来るようになってから、それを使って考える練習をするという
学習の流れが変わってしまったと思います。「それでも地球は動いている。」の再来を危惧します。
(数学は人の考えだけの世界だから、ユークリッド幾何と非ユークリッド幾何が在ります。
物理学の自然法則は人の考えに無関係だから、少なくともどちらかを実験で消去します。
現在、定量的に考察できるデータ取得ができず、それができない状態にあると思います。)
実際の測定の多くは間接測定ですが、間接測定(啓林館)の用語は学習指導要領解説にありません。
面積を間接測定するときの正しいものさしのあて方や計算の仕方まで、教えた方が良いと思います。
以下は、電卓を使用して面積を間接測定するときの計算方法です。理科の授業で思いつきましたが、
カシオミニの発売と同じころで、恩師が期待していた工夫(有効数字の省略算)ではなかったので、
授業では取り上げられませんでした。指導教員への苦肉の説明に学生実験で使ったことがあります。
今の指導教員が納得してくれるかは分かりませんが、「量も実数」としての扱いは大事と思います。
 (電卓使用時の測定値のかけ算の考え方。)
(電卓使用時の測定値のかけ算の考え方。)
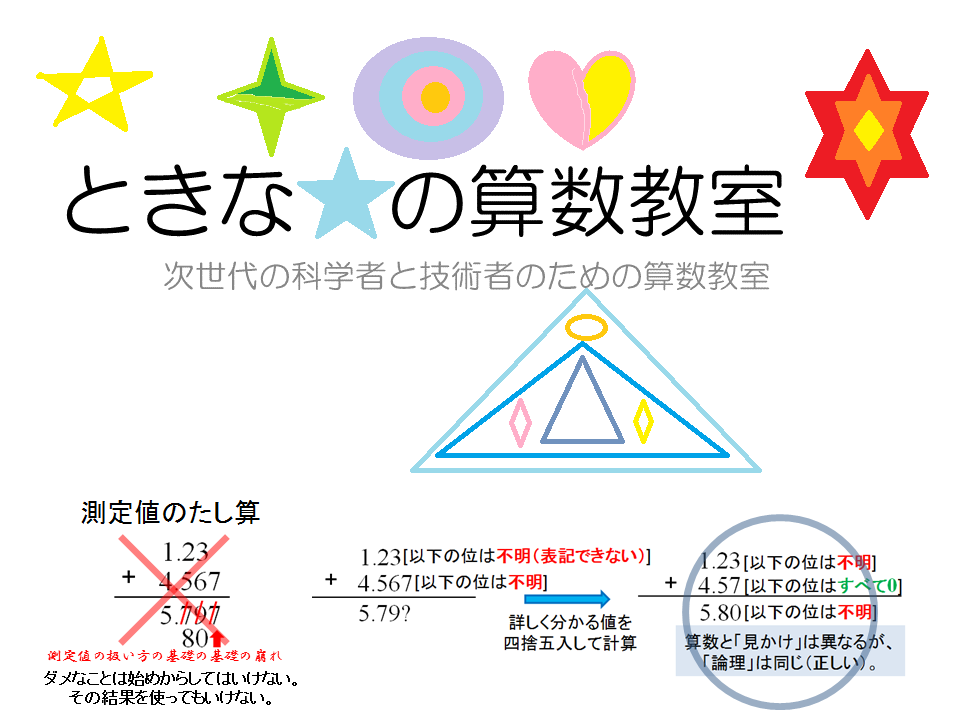
「測定値としての小数」と「数学につながる厳密な値としての小数」の計算のちがいの説明、特に、
たし算の違いを誤魔化さずに教えることは
間接測定を実践する力を育み、
無駄のない技術開発力を
育む大事なことと思います。考えの基となるデータが誤っていると正しい答えは得られません。
科学技術立国日本の再生には、大小や多少の量感に加え、実数としての量感育成も必要と考えます。
また、測定値の残差には有効桁がありますが、残差の意味の無い位まで使った意味の無い標準偏差を
使っての確率統計論的な説明も見られます。確率統計論の量の測定への応用は、実数としての量感が
十分育成できてからの方が教育費を含めた無駄が少なくなると考えます。(急がば回れと思います。)
物理学会2017年秋季大会発表(21pA42)の要約


「測定値のかけ算(0.00の二乗)」の要約シートへ
欧米の先進国から学び、それ以上のものを造り、電子立国日本となった。
新しい技術が開くとき、その理由を考えておくべきと思う。
第33回物理教育研究大会(日本物理教育学会年会2016)発表(2-a5)の要約

「約半世紀前の村上一中の理科授業はAL? −ズバリ測りましょう。工夫しなさい。−」の
要約シートへ
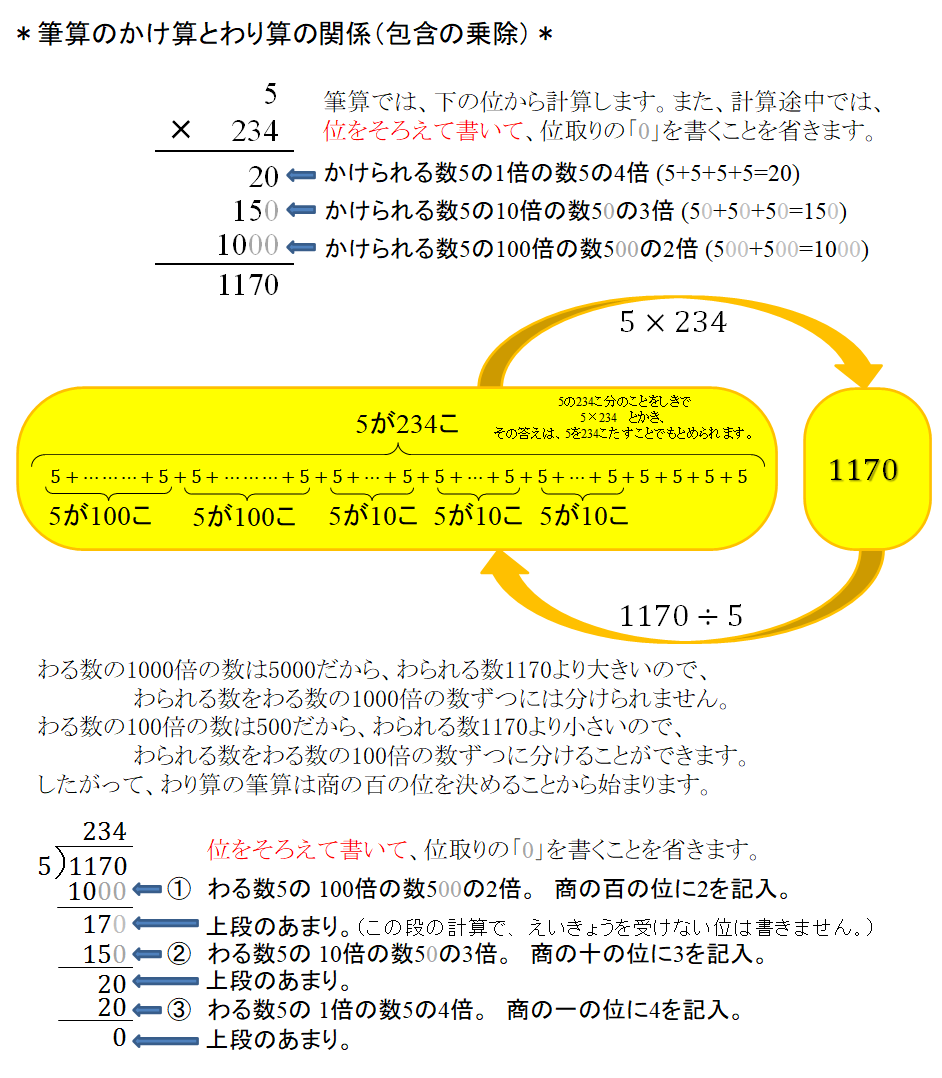
「ズバリ測る 」の掛け算と割り算の例(仮のゼロを使わない筆算の例)
研究開発費が沢山あっても、無駄遣いも多いと研究開発競争に勝てません。
ズバリ測る工夫を心がけることが大事と思います。


高専フォーラム2015発表の要約

「30年前にもあったアクティブラーニング」の要約シートへ
物理学会年次大会2015発表の要約

猿まね日本人と言われるほど、ものづくりが元気だったのは
測定値の扱い方が先進国に比べて上手であったことも一因と
考える。(測定機器が同じなら、測定値の扱い方が上手な方が
正しい情報を早く得る確率が高く、正しい情報を早く得た方が
早く開発できる確率が高いはず。)
発表シートの抜粋へ
高専物理のKS計画
1年生の第1回目の授業で、「平均値の求め方」など、測定値の話をするわけ:
高校生の研究発表会をときどき見に行きます。定量的考察にたえる測定値処理ができないため、
教育的ディベート練習の様な発表が多くなっているようにも見えます。定量的考察練習の土俵に
上がれて、はじめて、本当の考察の練習ができます。早く土俵に上がって、練習を十分積むこと
が大事と考えます。高専生は1年生から実験実習があり、早さが特に大事と考えるからです。
・わり算の筆算はインドネシアの方法(たのしい算数4上、大日本図書)が筆算原理も示した日本式の方法と思います。
インドネシアの方法について考察しておくと、理科で測定値を扱うときにも役立つと思います。
有効数字の前説明2 理科の四捨五入(考え方は算数と同じ。小数の違いから、サイコロをたまに使う。)
(注意) 学習到達度試験など、試験での有効数字については、問題文の指示を優先すること。
グラフから値を読み取る方法[最小二乗法(準備中)]
直接測定量から間接測定量[誤差の伝播則(準備中)]
物理学ノート「力と運動」の使い方

文字式を中学校で3年間習ったにもかかわらず、文字式を物理で使えない学生が多い。習ったことを
他の教科で活用する練習をすること。はじめは難しいので、第1章を習ったら写真の様に切り取って、
実験実習ほかの使えそうな科目の授業に持って行くと良い。
(必要部分集めにはレールファイルも便利。ものづくりは道具作りから、「あたまづくり」も同じです。)
高専教育フォーラム2014発表の要約

高専教育フォーラム2013発表の要約

高専教育フォーラム2012発表の要約

理科関連
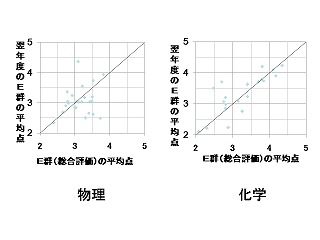
物理関連
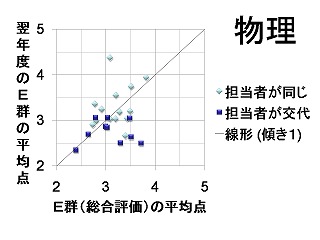
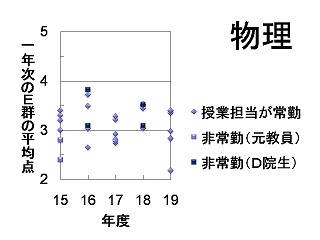
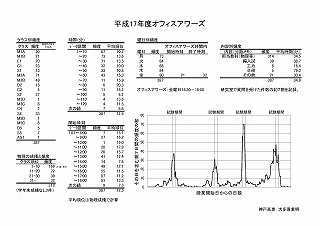
オフィスアワーズの記録

 ビデオ説明へ
ビデオ説明へ





 (電卓使用時の測定値のかけ算の考え方。)
(電卓使用時の測定値のかけ算の考え方。)




