
2.2 テスト波形によるウェーブレット変換とフーリエ変換の比較
時間周波数解析とは、通常の周波数解析に時間という次元を加えた解析である。その違いを明確にするため、図2.2.1(上)に示すテスト波形を用いる。テスト波形(上)、フーリエ波形(左下)、ウェーブレット波形(右下)それぞれの解析結果を比較するために、周波数軸、時間軸を同じスケールとした。この波形は表2.2.1に示すように周波数、現象開始時間、現象継続時間が異なる4つの波形を基本波形と合成したものである。

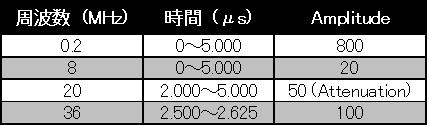
▼表2.2.1 テスト波形に含まれる周波数成分
フーリエ変換では、変換する時間内に含まれる周波数のパワーをその区間全てで積分して求めるため、その結果からは、振幅は小さいが現象の継続時間が長いのか、またその逆であるか判断することができない。
テスト波形のフーリエ波形だけを見てみると、8MHzと20MHzの持つパワーはほぼ等しくなっている。しかし実際は、発生している期間も異なり、さらに8MHzの波形が一定の振幅で発生しているのに対して20MHzの波形は減衰している。これらの情報は、テスト波形とフーリエ波形の両方を用いても完全には得ることのできないものである。
次にテスト波形をウェーブレット変換すると図2.2.1(右下)となる。テスト波形とウェーブレット波形を見比べてみると、ウェーブレット変換はフーリエ変換より周波数分解能が落ちていることが分かる。さらに、低周波数成分では周波数分解能が高く、時間分解能が低い。そして、高周波成分に対してはその逆になるという特徴があることが分かる。ウェーブレット波形より、20MHzの振幅が減衰している様子が確認できる。また、20MHzの現象は2.000μsから発生し、36MHzの現象は2.500〜2.625μsの期間に生じていることが確認できる。また、2.000、2.500、2.625μsの3点では、全周波数にわたりウェーブレット変換係数が見て取れる。これはこの時間に不連続点が存在すること、すなわち、新たな現象の生起時間であると特定することが可能となることを示している。得られたこれらの結果はテスト波形に含まれる周波数成分、生起時間とよく一致していることが理解できる。
以上のようにウェーブレット変換を用いると現象開始時間、現象継続時間の特定、時間的に変動する周波数成分の可視化が行えるので、従来の周波数解析であるフーリエ変換よりも、より詳細に考察していくことができる。