第２章　ウェーブレット変換

2.1　ウェーブレット変換手法

　ウェーブレット変換は連続ウェーブレット変換と離散ウェーブレット変換に大別され、前者はパターンや相違性の解析などに、後者はデータ圧縮やエネルギー解析などに応用されている。以下に本レポートで用いている連続ウェーブレット変換手法について説明する。
　ウェーブレット変換に用いられる関数は、ウェーブレット変換のすべてを特徴づける重要な関数でマザーウェーブレットと呼ばれており、局在を表す次の条件を満たす。

　一般に用いられるような遠くで速くゼロになる関数に関しては、同値となる次式が用いられる。

　この式は、が直流成分を持たない、すなわち振動的であるということを示している。
　本報告において使用したマザーウェーブレットは、連続ウェーブレット変換において広く用いられているGaborのマザーウェーブレットの一種である。Gaborのマザーウェーブレットを(4)式に示す。本レポートでは処理を相対値で行うことから定数を省き、σ=8とした場合の(5)式を用いる。このマザーウェーブレットの実数部分を図2.1.1に示す。

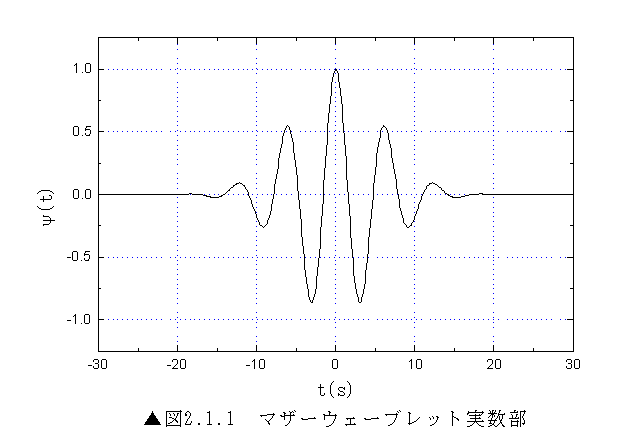
　ウェーブレット変換は、図2.1.1に示すようなマザーウェーブレットを横方向に拡大縮小し、さらにｔ軸上で移動させ、それと信号の積をとることにより、局所的な周波数を切り出している。この拡大・縮小・移動は変数ｔをスケールパラーメータとトランスレートパラメータによりと置き換えて、マザーウェーブレットをとした関数の組、

　すなわち、(6)式を積分核とした積分変換により行われる。ここでは周波数にあたり、は横軸の平行移動、すなわち実空間におけるウェーブレットの中心位置にあたる。ここでは各スケール・パラーメータにおいて同一のエネルギーとなるための正規化定数である。従って、関数のウェーブレット変換係数は(7)式のように定義される。

Back 　　Top　　Next
道平研究室TOP