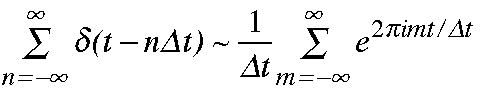
離散化関数、標本間隔、標本化周波数 次式(左辺)
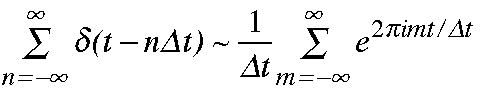
を離散化関数といいます。右辺はその複素フーリエ級数になります。
従って、このフーリエ変換対は次の関係になります。
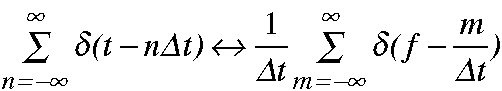
図にg(t)とそのフーリエ像関数G(f)の概念図を示します.
関数g(t)のΔt毎の離散化された関数を数学的に次で表します。
Δtは標本間隔、1/Δtは標本化周波数と呼ばれます。
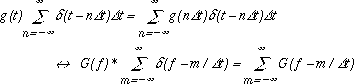
右辺はG(f)を1/Δt毎移動させて加算したものになります。Δt→0のとき左辺はg(t)になります。右辺はG(f)になります。下図にg(t)の離散化された関数とそのフーリエ像関数の概念図を示します.
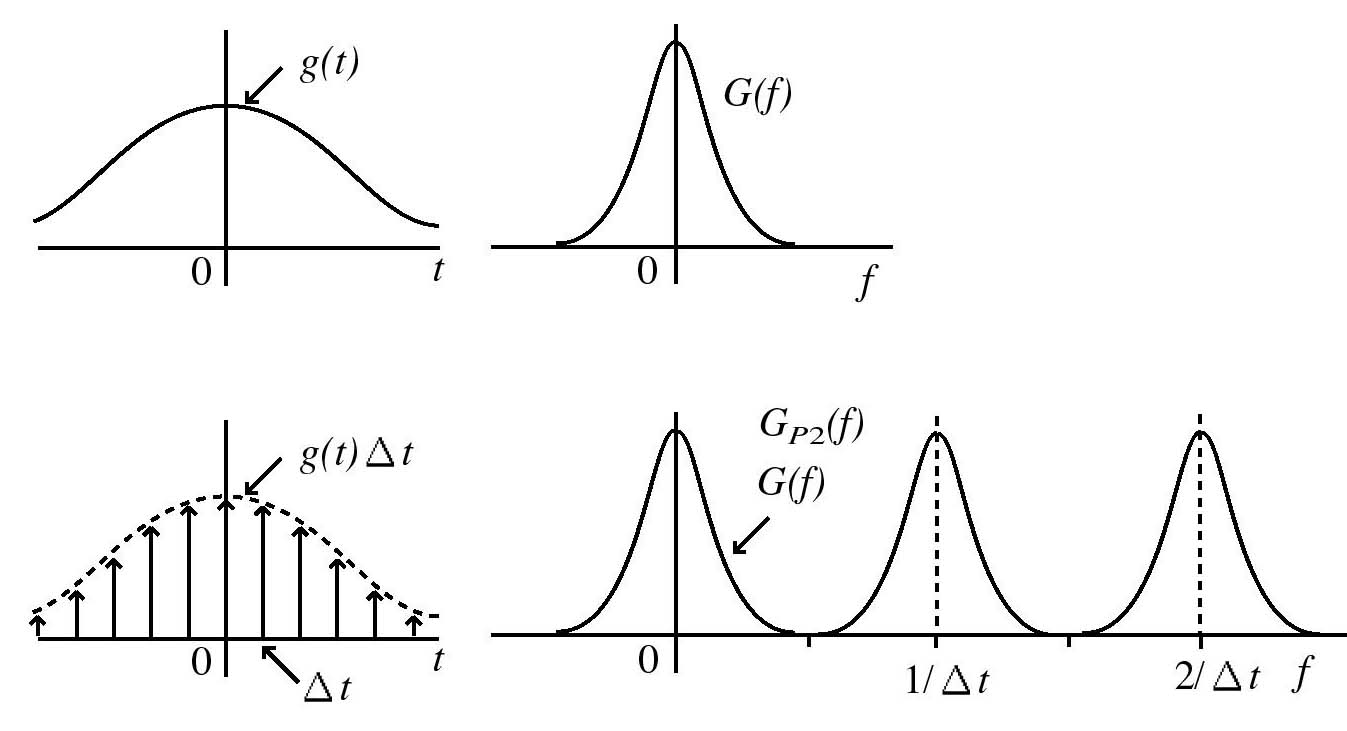
1/(2Δt)の周波数は折り返し(ナイキストNyquest)周波数と呼ばれます。
g(t)のフーリエ成分G(f)が図のように折り返し周波数未満までしか成分を持たない場合、離散化された関数を折り返し周波数未満まで通すローパスフィルタに通せば、元のg(t) に戻ることが理解できるでしょう。これが標本から元信号に戻す原理です。これを標本化定理と言います。しかし、g(t)のフーリエ成分が折り返し周波数を越えた周波数領域で成分を持つ場合、離散化された関数は折り返し周波数より高い周波数領域の成分を折り返し周波数より低い周波数領域に持つようになり、折り返し周波数未満まで通すローパスフィルタに通しても、元のg(t) に戻すことはできません。このような、折り返し周波数より高い周波数領域の成分が折り返し周波数より低い周波数領域にあることによる誤差を、折り返し(エイリアシングAliasing)誤差といいます。
⇒標本化定理の数学的表現