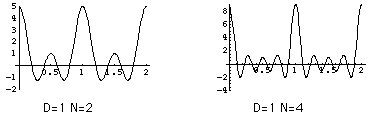(5.2)フーリエ変換の性質2

(5.2.1)フーリエ変換の性質2の利用1

移動体の速度測定

　移動物体の移動速度をvとします。この物体表面からの反射光を受信するセンサがある間隔Lで並んでいる、とします。あるセンサの受信信号をg(t)としますと、物体の移動方向の反対側一つ隣りのセンサの受信信号は、L/vだけ時間遅れの信号g(t-L/v)になります。
　2N+1個のセンサが並んでいるとし、その受信信号をすべて加算するとします。L/vをDと置き、加算した信号のフーリエ変換対を示します。

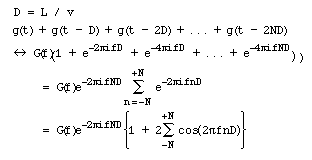
　{ }の中身をN=2の場合とN=4の場合で図示します。周波数軸のf=1/D=v/Lの整数倍のところにピークが発生します。Nが多くなるほどピークは高く鋭くなります。ただし、D=1とおき、周波数fは0から2/Dまでの範囲で表しています。 　表面からの反射光が表面の汚れや傷の影響を受けるとしますと、反射光はノイズとみなされ、広い周波数領域のフーリエ成分を持ちます。そこで、G(f)が f >> 1/D の領域まであるとしますと、加算した信号のフーリエ成分の絶対値はf=0とf=1/D=v/Lにピークができるようになります。ピークの周波数は速度vに比例します。この周波数v/Lより速度vが知られます。