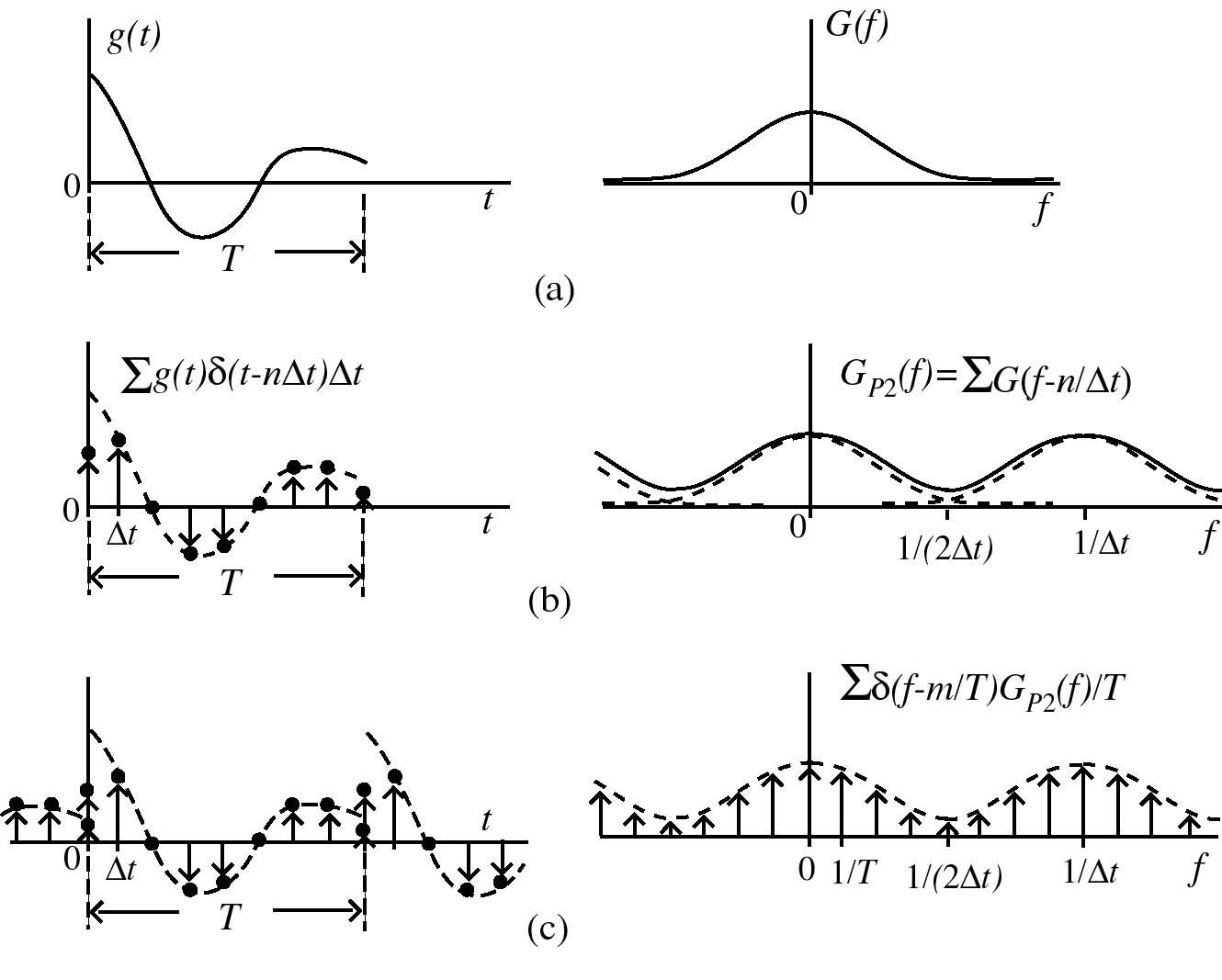
有限時間で打ち切られ済みの関数g(t)とそのフーリエ像関数の概念図を図(a)に示します.
g(t)のΔt毎の離散化された関数とそのフーリエ像関数の概念図を図(b)に示します。黒丸は標本を表します.不連続点での標本に注意.フーリエ像関数は1/Δt周期の周期関数になります.Δt→0のとき左辺はg(t)になります。右辺はG(f)になります。

次にフーリエ像関数を標本化します.その様子の概念図を図(c)に示します.
この標本化により,g(t)の離散化された関数は周期関数になります.
この場合,標本は時間関数およびそのフーリエ像関数において1周期分の有限個数で表現できることになります.
これらの標本の個数をNとおき,n番目をgn,Gnとおくとき次式が成立します.
あるいは,最初の式でGmを定義すると2番目の式が成立する.
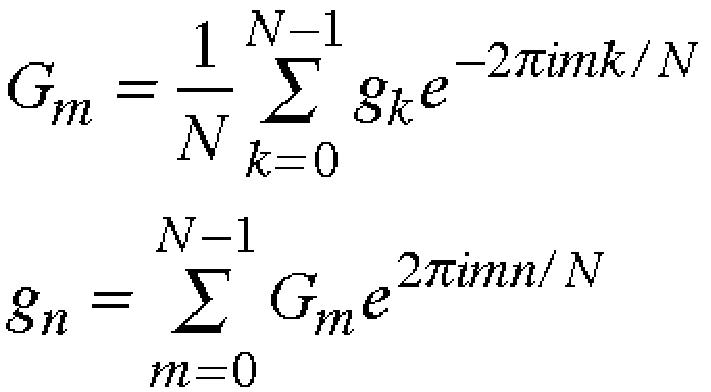
上式を,離散フーリエ変換,下式を離散逆フーリエ変換と言います.
(GnはG(f)の標本の意味ではないことに注意,gnは不連続点でg(t)の標本に一致するとは限らない).
⇒離散フーリエ変換の各種定義