(3)フーリエ級数

(3.3)フーリエ級数の性質3

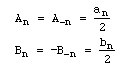
「フーリエ係数は周波数関数のサンプルといえる。」

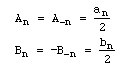
すると、フーリエ級数は次のように整数nを使って合成できます。
これは、これまでのフーリエ級数よりも見た目もスッキリしており、一般化したものになっています。

　-T/2〜T/2の範囲外でg(t)=0であるような信号g(t)を、下左図のように周期Tで繰り返したとき、
そのフーリエ係数は、ある周波数関数
（g(t)のフーリエ像関数G(f)の1/TであるG(f)/T）
の1/T間隔の標本
（An=real[G(n/T)/T]、Bn=-imaginary[G(n/T)/T]）
になっています。
これらを、下右図（概念図）で↑のように表しています。
ある一つの↑は、その周波数でのフーリエ係数を意味しています。